| Toto (situé au point A) veut aller chercher de l'eau à
la rivière (droite d) pour éteindre le feu situé
en B. Trace le chemin le plus court possible. 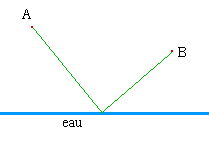 |
I Déroulement
Le problème a été exposé oralement la veille de
la première séance mais les élèves n'ont pas commencé
à le chercher.
Les élèves ont travaillé par binômes. Pour la première
séance chaque binôme a reçu deux fiches portant des figures
différentes et l'énoncé du problème. En voici un
exemple.
| Toto (situé au point A) veut aller chercher de l'eau à
la rivière (droite d) pour éteindre le feu situé
en B. Trace le chemin le plus court possible.  |
La deuxième séance a eu lieu une semaine plus tard. Les élèves,
placés devant la figure solution avaient pour consigne de trouver comment
cette figure avait été construite.
Après un bilan en classe, le lendemain, chaque élève devait
produire un petit compte-rendu .
II La séance de recherche libre
Les observations faites dans cette phase recoupent celles faites en quatrième. Deux binômes seulement se sont lancés immédiatement dans des essais de construction. Pour les autres, il y a eu deux attitudes.
La première se limite à chercher le chemin le plus court pour une position quelconque des points A et B ( parfois placés au jugé dans une configuration voisine de celle de la fiche ) et à annoncer le minimum trouvé : "le plus court chemin c’est 14 cm".
La seconde est celle des élèves qui ont conscience de l’insufisance de la première attitude mais restent perplexes, ne sachant pas quoi faire. Par exemple, une élève me dit : "il faudrait trouver quelque chose qui ne change pas dans la figure, mais quoi ?"
Après que j’aie eu précisé qu’il fallait trouver un moyen de construire le plus court chemin , deux types de recherche se sont dégagés : trouver des idées de construction et les tester ou placer le point M au minimum de la distance affichée et explorer les propriétés de la figure en faisant divers mesurages.
Cette première séance fait apparaître un certain nombre de difficultés
La recherche libre avec cabri est complexe et les élèves les plus faibles peuvent vite patauger.
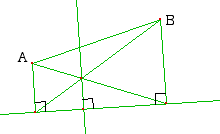
Pour prendre un exemple, des élèves ont produit la figure suivante :
: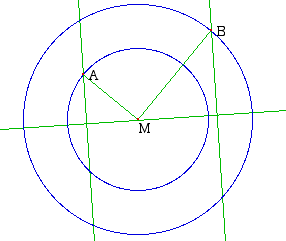
où M est un point mobile sur la droite placé à vue au mimimum de MA + MB .Voilà bien le genre de figure qui fait frémir le prof d'espoir. En vain. En fait ces élèves cherchent à placer M à égale distance de A et B, et pour cela vont déplacer B ou A (M étant considéré comme "bien placé").
Beaucoup d' essais visaient, comme celui-ci à placer M à équidistance de A et B
Cabri est décevant en ce qui concerne les angles, piste suivie par plusieurs binômes. Le chemin minimum correspond au cas où les angles d'arrivée et de départ sont égaux, or cela n'apparaît pas à l'observation, car il y a un petit intervalle et non un point pour lequel la somme des distances affichée est minimale. Pour faire mieux, il faudrait afficher plus de deux chiffres après la virgule mais dans ce cas l'affichage simultané des longueurs et des angles rend l'écran illisible
Le meilleur travail a été celui d’élèves alternant des moments de travail papier-crayon, pour expliciter leurs idées et travail devant l' ordinateur pour les tester. En fin de première séance le binôme le plus avancé avait éliminé la plupart des conjectures habituellement avancées , d’autres en étaient à élaborer une première conjecture …
III Recherche d'une construction à l'aide du fichier solution
Les points A et B étant les seuls mobiles la "traversée de la rivière " pouvait-elle mettre des élèves sur la voie ? Dans la figure donnée, le segment AB était tracé en pointillé, de façon à faire apparaître le chemin le plus court lorsque A et B sont de part et d'autre de la droite.
|
|
|
|
|
Le fait a été constaté, et parfois commenté ( "ben là évidemment c'est la ligne droite"), mais personne n'en a vu l'intérêt.
De cette séance, je retiens deux points positifs
- La situation est suffisamment simple pour que tous s'engagent dans une activité
de production et tests de constructions.
- La figure construite permet des observations plus fiables que dans la recherche
libre. Elle permet par exemple de vérifier l'égalité des
angles ( d'incidence et de réflexion) et il apparaît plus clairement
que le minimum est atteint en un point.
Cependant la séance est plus intéressante pour les élèves qui n’avaient pas eu le temps de tester beaucoup de constructions lors de la première heure de recherche, ceux qui avaient déjà éliminé plusieurs conjectures "sèchent ", à court d'idées.
Une difficulté plusieurs fois rencontrée est l'utilisation du
point M donné ( le point solution) pour faire une construction censée
aboutir à M !
Un binôme fait la conjecture suivante
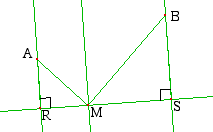 |
La bissectrice de AMB est parallèle à AR et BS |
Finalement une solution a été trouvée mais ce n’était pas celle que j'espérais.Elle l'a été par un élève exclu de l'ordinateur, pour non-respect des consignes.
| Après 20 minutes de travail très concentré sur une petite figure, il m'appelle pour me proposer la conjecture suivante | 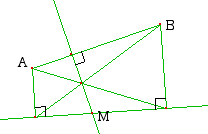 que je l'invite alors à tester sur ordinateur. |
La rectification est quasi immédiate |
 Ca marche !!! |
Cette solution économique, idéale sur le plan pratique, a un
inconvénient majeur :sa preuve n’est pas à la portée
des élèves de cinquième et utilise de toutes façons
la solution par symétrie(voir annexe). Il ne me restait plus qu'à
mettre les autres sur la voie en déclarant : une solution a été
trouvée, masi il y en a une autre.. qui utilise la symétrie !
Presque tous les binômes ont la réponse en moins de deux minutes,
et c'est une illumination. Dans les cinq dernières minutes, on a eu le
temps de mettre les deux solutions au tableau, et les élèves ont
pu vérifier leur concordance sur la figure.
IV Bilan et compte-rendus
Pour la clarté de ce qui suit, il faut savoir que la plupart des élèves
ont rebaptisé le point A : Toto ou T et le point B : Feu ou F. L'explication
de la solution par symétrie a été donnée au tableau
par des élèves, sous la forme
"Le chemin TMF est équivalent au chemin T'MF et celui-là c'est
le plus court parce que c'est la ligne droite".
Je me suis contentée de préciser : si on prenait un autre point M, le chemin symétrique ne serait plus en ligne droite… J'ai ensuite guidé les élèves pour démontrer que la bissectrice de l'angle TMF est perpendiculaire à d (une des conjectures produites).
Et j'en ai profité pour leur signaler que c'est une loi de l'optique mais ils n'en ont rien eu à cirer : ils préférent nettement l'histoire de toto
Dans ce genre de travail, les compte-rendus apportent, on va le voir, plus d'information que la simple rédaction d'une réponse au problème. J'ai donné une consigne assez vague : le compte-rendu doit permettre de savoir ce que vous retenez de ce travail.
Les résultats ont donc été assez variés : simple
explication de la solution, avec parfois la démo sur les angles , explication
de la solution avec description de la recherche effectuée et même
nouvelle recherche du problème à l'aide de la règle graduée
…
Quelques élèves valident la solution trouvée par mesurage,
et parmi ceux-là il y a deux réponses fausses donnant comme minimum
le point équidistant de A et B. Un des élèves la présente
comme une deuxième solution .. Cela me met la puce à l'oreille.
Si tous se sont déclarés convaincus par l'explication de la solution
par symétrie, certains en sont restés à l'idée de
trouver une distance minimale, sans réaliser que ce minimum était
atteint pour un point et un seul. D'ailleurs un seul compte-rendu explique pourquoi
le chemin serait plus long pour n'importe quel autre point . Le retour à
la règle graduée a fait le reste.
En rendant les compte-rendus, j'ai demandé
Le chemin trouvé par symétrie est le chemin le plus court possible,
mais est-on sûr qu'il n'y a pas un autre chemin égal à celui-là
?
la classe s'est alors partagée. Une bonne moitié doute (en partie
par effet de contrat : si elle nous pose la question, il y a anguille sous roche),
les autres emploient tous l'argument : si on prend un autre point, il n'y a
plus l'alignement et emportent rapidement l'adhésion des premiers.
Conclusion
Les élèves de cinquième ne butent ni plus ni moins que les élèves plus âgés sur ce problème. En fin de cinquième, les connaissances nécessaires sont en place, et ce problème permet de retrouver la problématique du "triangle plat":
Il y a une fois de plus contradiction entre le mesurage et la preuve logique, mais cette dernière ne s'en tire pas trop mal. Avantage collatéral : une petite démonstration utilisant le calcul littéral
Remarque : la conjecture de la bissectrice a vraiment peu de chances de sortir lors de l'envionnement cabri !
Scénario d'utilisation
Une recherche appuyée par un logiciel de géométrie dynamique
nécessite des allers-retour entre travail papier -crayon et travail devant
l'ordinateur. De plus des moments de formulation et de mise en commun sont indispensables.
Or très peu de salles d'informatique disposent d'un espace de travail
hors écran. Le plus souvent, elles sont conçues pour un tête
à tête élève-écran.
Le mieux serait de disposer, en salle de mathématique, de quelques ordinateurs,
accessibles aux élèves selon les besoins.
En attendant… dans la première partie de la recherche, la figure
animée n'est pas indispensable, bien qu'elle puisse permettre une compréhension
plus rapide du problème posé. Les élèves peuvent
tout aussi bien tester des chemins à la règle graduée,
sur des figures qu'ils font eux-mêmes, pour avoir une variété
de cas. Après une mise en commun des conjectures, une seule séance
avec le fichier solution peut suffire.