Retour
Algorithme de Dijkstra
Edgser Wybe Dijkstra
(1930-2002) a proposé en 1959 un algorithme de recherche de
chemin minimum dans un graphe dont la
complexité est en O(n).
Il est à noter que l'algorithme donne le plus court chemin
de la
source à tous les sommets du graphe, y compris, bien
sûr
au but !
Explications
Un graphe pondéré, orienté ou non
étant donné.
Initialisations
Au
démarrage, on place tous les sommets du graphe dans un
tableau ;
On affecte au sommet source S la valeur 0 et à tous les
autres sommets la valeur "infini". En pratique, on choisira une valeur supérieure à toutes les valuations.
Fonctionnement
Soit S1 le sommet de plus petit coefficient ; on note le sommet S1 comme terminé ; en pratique on rayera toutes les cases de la colonne de S1.
pour tous les sommets adjacents à S1 faire :
c:=
valeur de S1 + poids de l'arête reliant S1 à Sn
Si c
< valeur de Sn alors on
écrit dans la case de Sn : c et S1 qui signifie que le
chemin de
coût c amène de S1 à Sn
Sinon,
recopier ce qui se trouvait dans la ligne
précédente
compléter la ligne du tableau en recopiant les valeurs de la
ligne précédente.
Recommencer tant qu'il existe des sommets non encore
sélectionnés
La plus courte distance entre S et Sk se lit en "remontant" la
chaîne.
Exemples
Pour commencer, jouons l'algorithme sur un graphe d'école :
Dans ce cas, on pourra écrire le fonctionnement de l'algorithme dans un tableau ; chaque case comportant d'une part la longueur pour atteindre le sommet de la colonne et d'autre part le sommet précédent. La longueur est minimum lorsque le reste de la colonne est colorié.
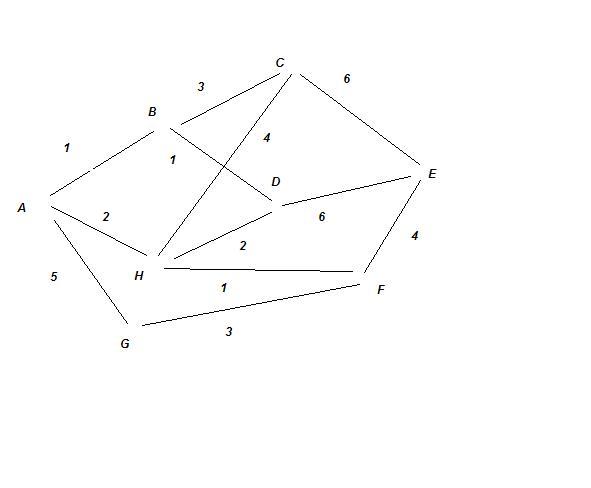 |
Le départ (source) est en A.
Dans chaque case du tableau, on indique d'une part la longueur du
chemin venant de A, mais aussi de quel sommet on vient pour obtenir ce
résulltat
| A |
B |
C |
D |
E |
F |
G |
H |
0
|
inf
|
inf |
inf
|
inf
|
inf
|
inf
|
inf
|
|
1 -A |
inf |
inf |
inf |
inf |
5 -A |
2 -A |
|
|
4-B |
2-B |
inf |
inf |
5-A |
2-A |
|
|
4-B |
|
8-D |
inf |
5-A |
2-A |
|
|
4-B |
|
8-D |
3-H |
5-A |
|
|
|
4-B |
|
7-F |
|
5-A |
|
|
|
|
|
7-F |
|
5-A |
|
|
|
|
|
7-F |
|
|
|
Pour aller de A à E, le chemin le plus court est de longueur
7, et :
E vient de F qui vient de H qui vient de A : A - H - F - E
On remarque que cet algorithme donne tous les plus courts chemins au départ de A.
Pour tester d'autres parcours cliquez ici
|
Compliquons un peu les choses avec la recherche d'un plus court chemin
dans le graphe des transports en commun lyonnais ; le plan ci-dessous
donne les lignes de métro, tramway et bus Cristallis de
l'agglomération lyonnaise ; je suis à Vaulx la Soie et je veux aller à Montrochet le plus vite
possible.

Ce plan de Lyon avec quelques lignes pertmet de mettre en oeuvre
l'algorithme :
On considère le graphe ayant comme sommets les stations
offrant
une correspondance et comme arêtes les lignes rejoignant ces
stations. On pondère les arêtes par le nombre de
stations
; on ne tiendra pas compte dans un premier temps des changements. Le graphe peut
être
représenté par :
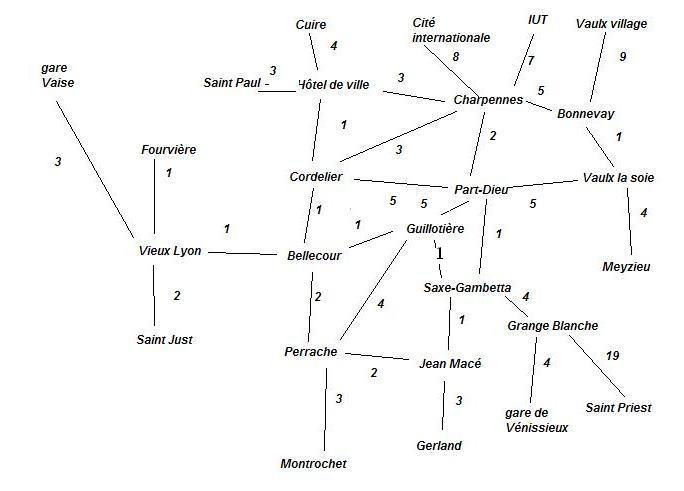
En appliquant cet algorithme, on peut aller de Vaulx la soie à Montrochet en suivant le chemin :
Part-Dieu
Saxe-Gambetta
JeanMacé
Perrache
Montrochet
de longueur 12.
Pour tester vous-mêmes d'autres parcours
Pour perfectionner le modèle, il faudrait, bien sûr, compter un temps supplémentaire lors des changements de lignes, et sans doute aussi pondérer les valeurs des arêtes suivant le mode de transport, le métro étant plus rapide que le bus, par exemple. Le principe est toutefois le même, même si le graphe traité est plus grand !
Retour