Retour à la page précédente

Constructions d'un heptagone régulier

L'heptagone régulier n'est pas constructible à la règle et au compas, (première démonstration), (deuxième démonstration), mais il existe des constructions qui en donnent une très bonne approximation.
En voici deux, la première peut être proposée en seconde, la deuxième peut être en terminale une application des nombres complexes.

Scénario proposé :

  1. Construction de la figure à la règle et au compas
  2. Test à l'aide d'un logiciel de géométrie
  3. Calculs
Première construction
Niveau seconde
Construction d'un heptagone régulier


Tracer un cercle, placer un point M sur ce cercle et tracer un deuxième cercle de même rayon et de centre M. Reporter sept fois sur un cercle la demi-corde commune.


Cette construction est-elle exacte ?
Deuxième construction
Niveau Première terminale
Construction d'un heptagone régulier


Tracer un carré et un triangle équilatéral ayant un côté commun. Le cercle inscrit dans le carré coupe un côté du triangle équilatéral en M.
I étant le milieu de [AB], la longueur MI est celle du côté de l'hetagone.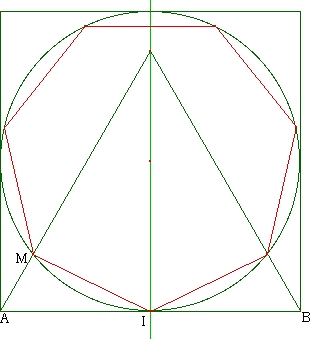


Cette construction est-elle exacte ?
En clin d'oeil : une superbe animation sur le site abracadabri

Le découpage d'un heptagone en sept heptagones identiques

 Deux tests de la deuxième construction :
  • Test1 : On reporte cinq segments de même longueur on joint le septième sommet au premier.
  • Test 2 : On reporte six segments de même longueur.
Calculs !