Retour à la page précédente

Deux "théorèmes"

Lisez attentivement la démonstration du premier.

Si un quadrilatère convexe a deux côtés opposés de même longueur, c'est un trapèze (isocèle).

Démonstration :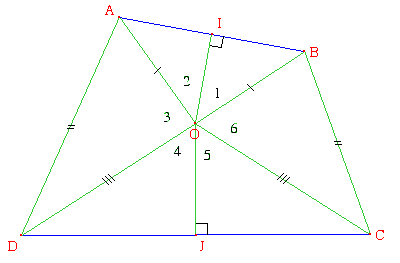
Soit un quadrilatère ABCD tel que AD=BC. Nous allons prouver que (AB) // (CD).
Soit O le point d'intersection des médiatrices de [AB] et [CD].
O étant un point de la médiatrice de [AB], le triangle OAB est isocèle en O, donc OA = OB et Ô1=Ô2.
O étant un point de la médiatrice de [CD], le triangle OCD est isocèle en O, donc OC = OD et Ô4=Ô5.


Les triangles OAD et OBC ont leurs trois côtés respectivement égaux, donc ils sont isométriques (superposables), par conséquent Ô3=Ô6.
On a donc Ô2 + Ô3 + Ô4 = Ô1 + Ô6 + Ô5 .
Comme la somme de ces six angles est égale à 360°, on en déduit que Ô2 + Ô3 + Ô4 = Ô1 + Ô6 + Ô5 = 180°, donc les points I, O, J sont alignés.
Les côtés [AB] et [CD] ont donc la même médiatrice, ce qui prouve que (AB) // (CD).

Vous ne voyez rien qui cloche ? Alors passez au suivant.

Tout triangle est isocèle

Démonstration :

Soit un triangle ABC. Soit O le point d'intersection de la médiatrice de [BC] et de la bissectrice de l'angle Â.
Traçons les perpendiculaires à (AB) et (AC) passant par O. Elles coupent respectivement (AB) et (AC) en H et K.

Tout point de la bissectrice d'un angle est équidistant des côtés de cet angle. On a donc OH = OK.
Considérons les triangles rectangles OAH et OAK. AO est leur hypoténuse commune et OH = OK, donc, d'après le théorème de Pythagore, AH = AK.
Considérons maintenant les triangles rectangles OHB et OKC. Comme O est un point de la médiatrice de [BC], OB = OC. On a donc de la même façon HB = KC.
Or AB = AH + HB et AC = AK + KC. Conclusion : AB = AC. Le triangle ABC est donc isocèle en A.

Vous êtes perplexe ? Essayez de trouver le maillon faible, avant de regarder les figures cabri