La longueur de la ligne brisée ne tend pas vers celle du segment (égale à 1), puisqu'elle reste constante, égale à .

C'est sur le sens de l'affirmation « la ligne brisée tend vers le segment [AB] » qu'il faut donc s'interroger.

On peut montrer que la longueur de la hauteur des triangles est une suite géométrique de raison ½ qui tend donc vers 0. Ainsi l'écart maximum entre les deux courbes, ligne brisée et segment, tend vers 0.

On peut montrer que l'aire de la surface qui sépare ligne brisée et segment est aussi une suite géométrique de raison ½ (à chaque étape, on a deux fois plus de triangles, chacun d'aire divisée par 4) qui tend donc vers 0.

Pour autant les deux courbes ne convergent pas en longueur. ...

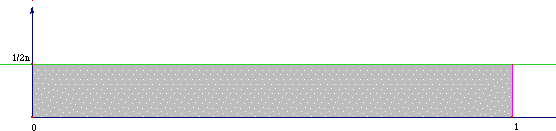
Vous n'aurez pas de difficulté non plus à trouver une famille de courbes qui tend vers le segment [0, 1] , et dont la longueur reste égale à

Il y a plus fort ! Trouver une famille de courbes dont la longueur tend vers l'infini quand l'aire du rectangle tend vers 0.