Du triangle au rectangle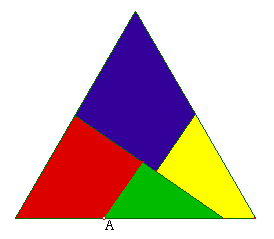
De l'hexagone au rectangle
Quelques problèmes à différents niveaux
- En sixième-cinquième, un problème de construction ( utilisation des angles, ordre de construction)
- Aire et périmètre
en troisième.
On sait que la confusion aire-périmètre persiste longtemps. Le puzzle animé est de ce point de vue très déstabilisant : tout semble changer dans le rectangle. Le problème proposé exige un peu de calcul avec des radicaux.
Pour faire varier le côté du triangle, il faut dépunaiser un sommet du triangle, ce que vous pouvez faire après avoir téléchargé le fichier cabri. (Les élèves peuvent ainsi valider leurs formules) - En première S
En partant du problème de géométrie, l'énoncé guide les élèves dans une étude de fonction où l'on retrouve le carré comme rectangle de périmètre minimum pour une aire donnée..